在相同的英文字（s、p、d、f)時
數字越高，逕向分布圖上的波浪數就越多，並且越後面出現的波會越大
但不會超過前一個圖形的最高峰

畢竟這是電子出現的機率，所有面積加起來要100%
⇒ 1s的浪高會是最高的，因為2s、3s的浪高都被分散了

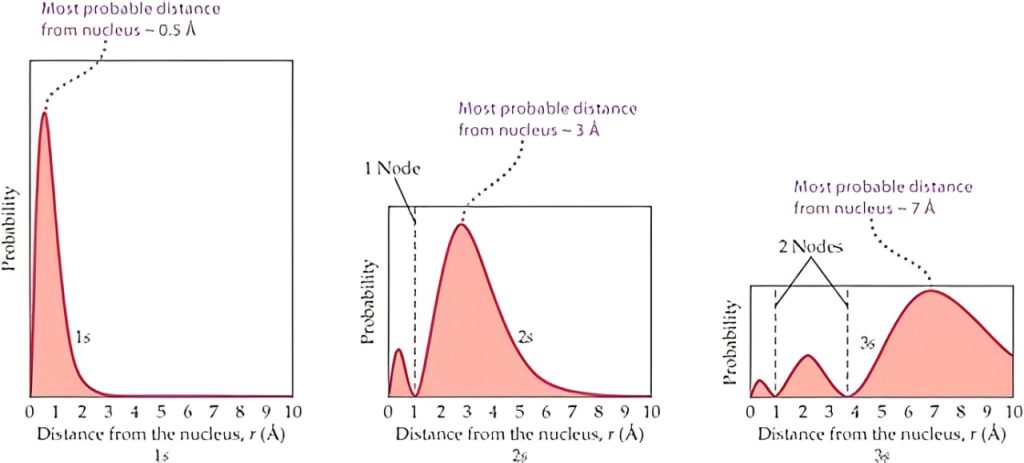
隨著數字增加，電子最可能出現的地方越外圈（但不代表內圈就沒有，而是機率下降）
⇒ 相同類型的原子軌域，數字越大，電子離原子核的距離越遠

將上面三張圖（1S 2S 3S 軌域），放一塊比對

接著來看 d軌域（3d 4d 5d），比對一下上面的圖，會發現「這些特徵」也完全相同

再來將相同數字的（3d 3p 3s）放在一起比對
會發現「疑，奇怪？」，為什麼3s能量最低，最高峰處卻離原子核最遠？

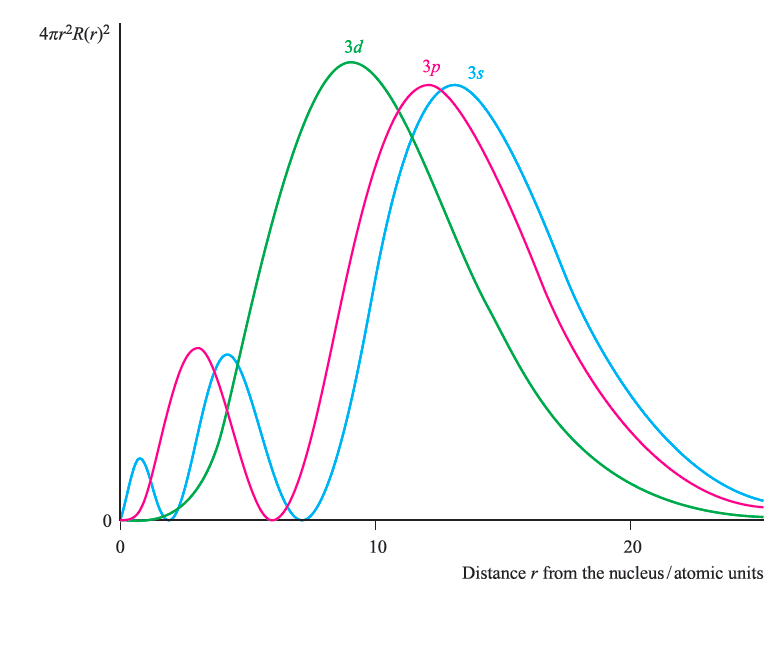
3s 雖然機率高峰在更遠處，但也有兩個較小波在近處
所以整體平均來說（按照機率、距離，加總計算）是最靠近原子核的

用樂透抽獎跟錢＄＄來比喻的話，ex: 越靠近原子核的獎金越高
以3d居民來說，因為高峰處更靠近原子核
大部分獎項落都在1000元，乍看之下比3s居民高

可對3s來說，雖然大部分獎項落在800-900元，普獎少了一些些
但是人家有非常多的機會參加二獎、頭獎！大約有10%的人能中二獎（1萬元）、以及5%左右的人能中大獎（10萬元）

相比之下，3d能參加頭獎、二獎的人卻微乎其微
算上這些，整體來說3s主委加碼的力度更夠！
其中「3s更容易中大獎的」的這件事情，就是「穿透效應」！

穿越其他外層電子的機率，從而更靠近電子核，感受到較多的核吸引力的現象（感受較多主委加碼的力度）

當n固定時，l越小，則峰越多
而且它的第一個峰離核越近（或者說第一個峰鑽得越深），這就是軌域鑽穿效應

用2s 2p的圖來看也是如此，2s的高峰處比2p來得遠
但把靠近原子核的部分，細部放大來看，就又有人(2s)鑽進去了！

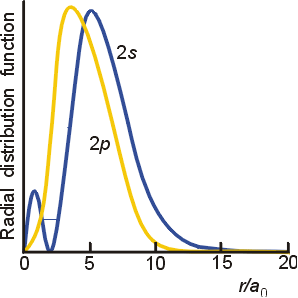
可以很清楚看到
2s的主委加碼的很用力、2p的主委真的沒錢加碼（名額少得可憐）

2s主委：今天要狠狠加碼一下

想像成「原子核」就是「胡瓜」就對了

綜藝節目常常圍繞著一堆看表演的民眾
外圍吃瓜群眾一大群、圍著一圈又一圈的，
此時越靠近主持人胡瓜就有機會拿到超大獎

「穿透效應」就是穿透人群（電子雲），偷偷地擠進內圈抽大獎

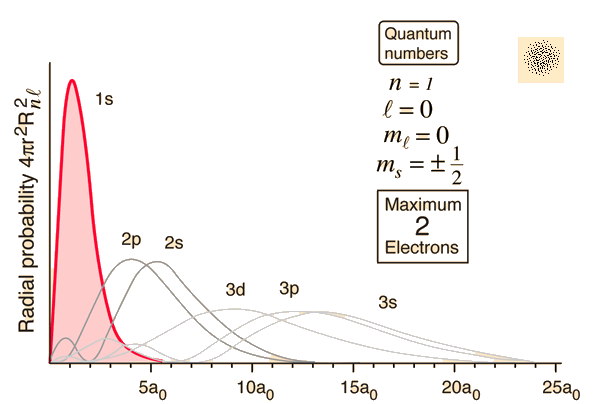
最後大雜燴，將所有常見軌域放一塊比較