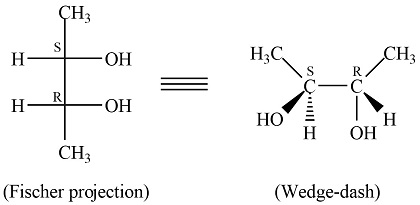
當初有機學到這,我興高采烈跟朋友說我學會看「魚骨圖」了!
朋友:「???」
後來發現這根本不是魚骨圖(Fishbone Diagram)
只是 Fischer 名稱像 Fish🐟、畫出來結構形狀像「魚刺」而已
之所以稱之「費雪投影」,是因為發明者的名字
赫爾曼·埃米爾·費雪(Hermann Emil Fischer, 德國有機化學家) 提出來的模型,用來描述立體異構物
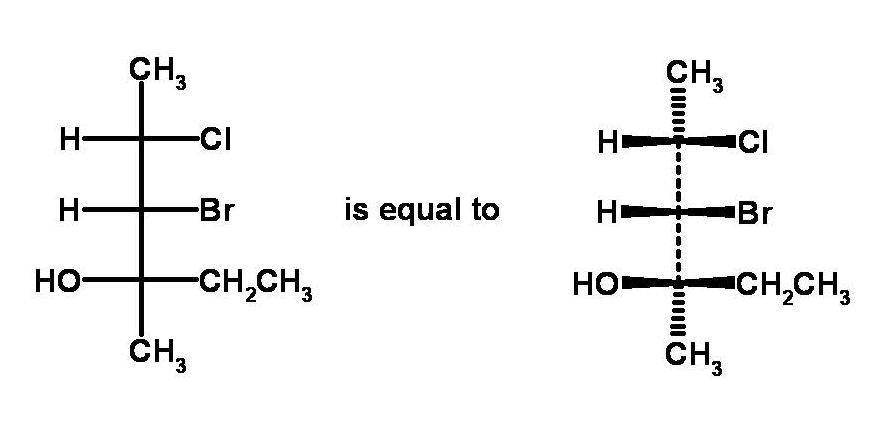
當初,立體分子結構不好畫、太複雜,畫完就天黑了
所以要找一種「簡畫法」 ,可以用來描述立體空間
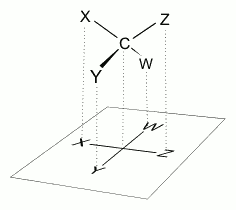
Fischer 投影訂出一套規則:
使用「2D 十字架」來表示立體分子
垂直線(上下)= 遠離觀察者(往後)
水平線(左右)= 朝向觀察者(往前)
此圖ABCD基團是立體結構
AB在鼻中膈(臉的中線平面上),最遠離眼睛
C突出紙面、D陷入紙面,分別對應到左眼、右眼(就是紙面的上方、下方)
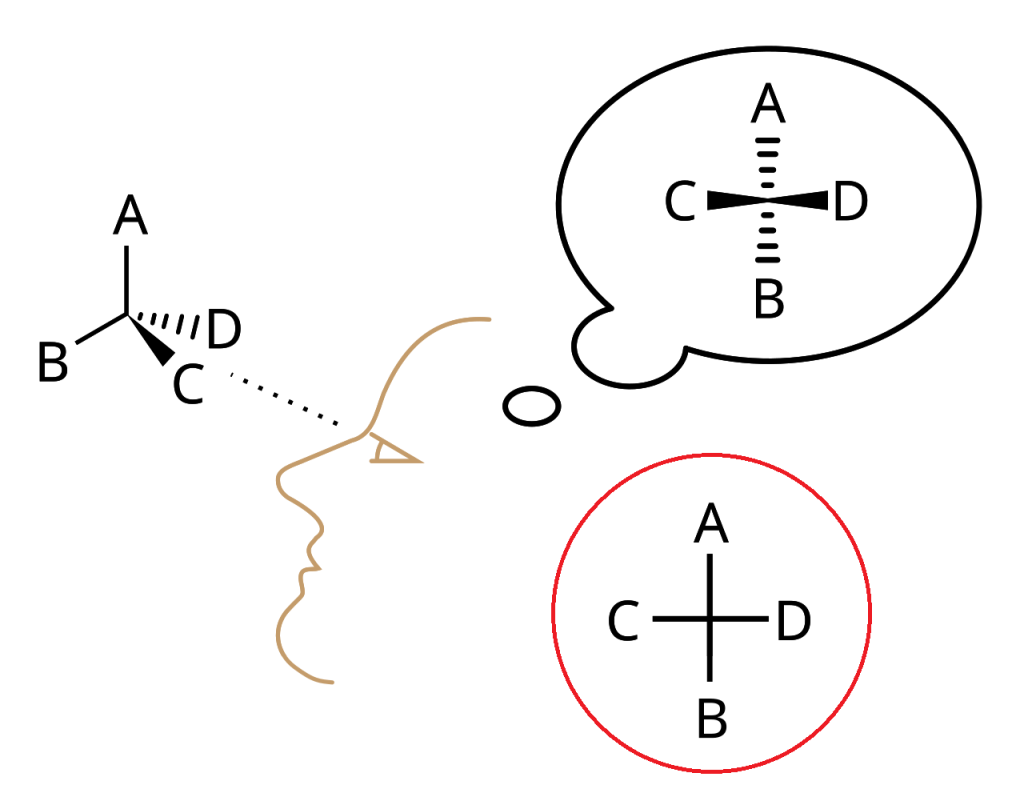
依此人的立場(觀察者的角度)而言,他觀察到的結構是他右上角所想的樣子
所以他畫出來的費雪圖,就是紅圈處
(A = 上、B = 下、C = 左、D = 右)
然而對於我們來說卻是不同的視角,會覺得圖像「長得不一樣」
為了讓所有人能統一描述,於是規定一個分子的「拿法」:
想像手裡有一根碳鏈(真實的3D結構)
將分子的主鏈 (C–C–C…) 豎直拿起來,讓最氧化的基團(CHO/COOH)在最上面
大家視角相同,那麼畫出來的圖就會相同
除了拿的時候拿反了(頂端、底端對調)之外
此時只要扭個脖子、上下顛倒看,就能發現他們是一樣的東西
費雪投影中間的C
投影中心(中間交點、交會處)是碳(C),一定是sp³ 四面體型(C向外伸出四隻手)
然而此處的C有可能是C*(具有chiral center, 掌性中心)、有可能不是
以甘油醛 (glyceraldehyde) 為例:
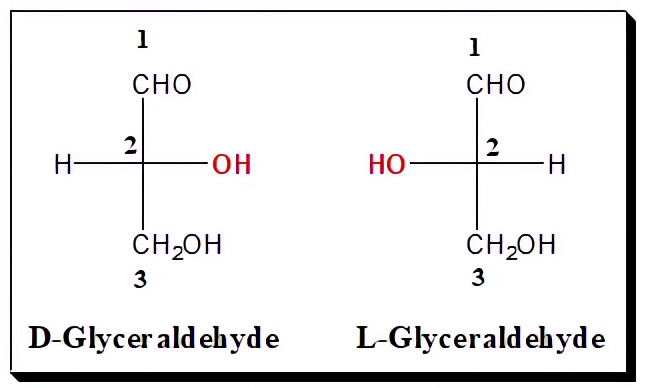
C1 = CHO(sp²,不是掌性中心)
C2 = C* (sp³,連接的四個基團都不同 (H、OH、CHO、CH₂OH) → chiral center)
C3 = CH₂OH(sp³,連接的兩個 H 相同 → 此C具有對稱性 achiral center)
其中,因為 C2 是 C*
此位置上可有不同的接法 ⇒ 造就了整體兩個不同分子(D/L異構體)
話說有個疑惑:費雪投影上所有的C都是 sp³ ?那豈不是只有單鍵嗎?
如果分子出現雙鍵怎麼辦?
答案是:sp² 帶雙鍵(π 鍵)的碳一定不會出現在中間交點
只可能寫在主鏈的端點(頭 or 尾)
因為費雪投影是「2D平面展示 3D立體構型」,
如果 sp² 帶雙鍵(π 鍵)的碳出現在「中間」,
那麼他最多只有三個基團、絕對不可能成為「掌性中心」
三個基團的中心原子(平面葉扇狀,120°)不會有R/S form,不存在左/右旋的差別,所以不需要辨別立體構型
那麼也就失去畫費雪投影來辨別的意義
所以,所有不能畫成 Fischer 投影的分子,都沒有「sp³ 掌性中心異構物」
就是不用擔心會有以下這樣畫的
因為這些只能用骨架式結構(Lewis 結構)呈現,而非費雪投影
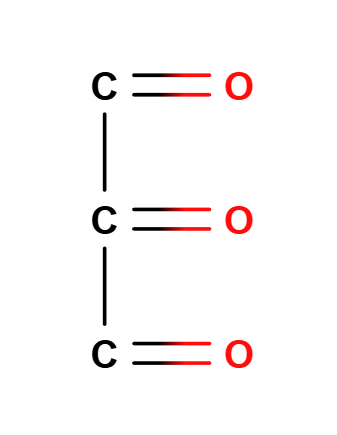
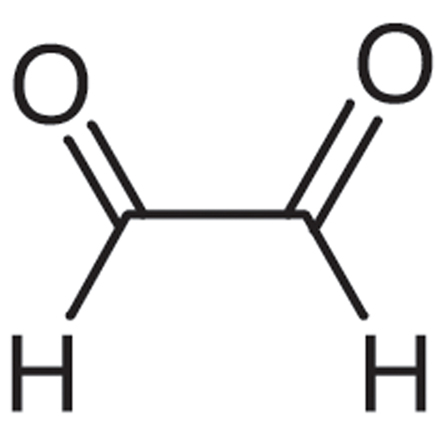
Glyoxal(乙二醛, OHC–CHO)
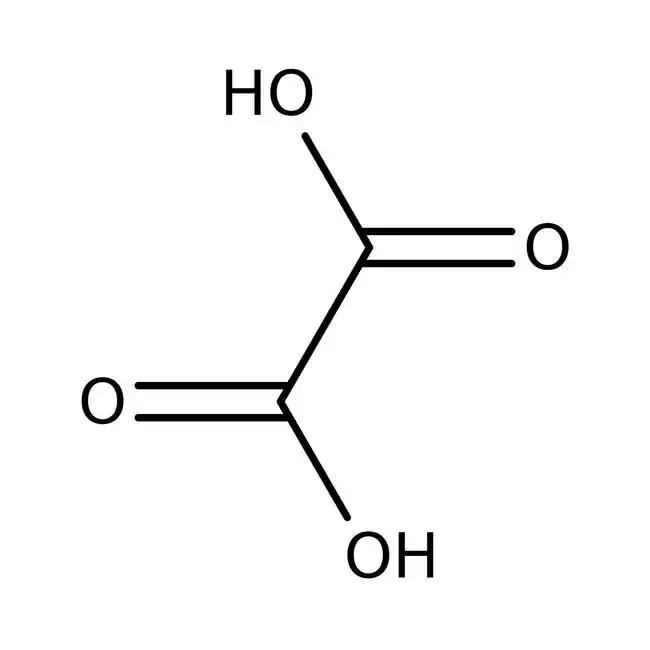
Oxalic acid (草酸, HOOC–COOH)
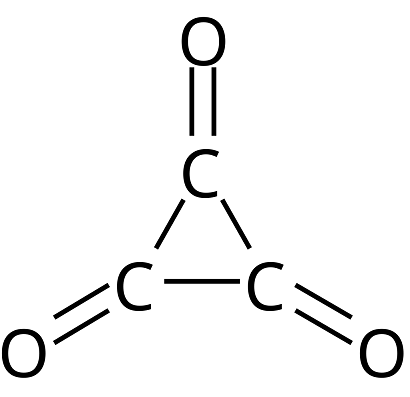
Cyclopropanetrione/Trioxocyclopropane(環丙三酮, C3O3)
費雪互換操作
「同一個C上的基團可以進行交換」,但是不能與主鏈上其他的碳進行交換,否則會改變骨架
任意交換一次(奇數次)構形會翻轉(R → S 或者 S → R)
任意交換兩次(偶數次)會與原本構形重疊(相同)
此圖A跟H互換、B跟H互換,總共互換兩次,構型會與原本相同

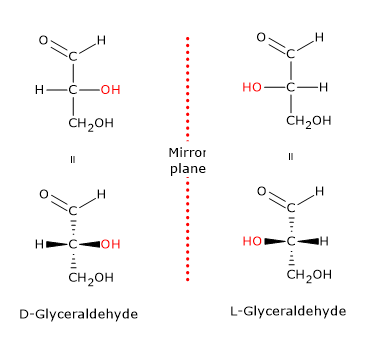
然而以下幾個例子則不然,構型不同、會出現 D/L form:
這圖杯壁無比,
看起來稍微將圖左右翻轉就可以得到,但這兩個是對映異構物
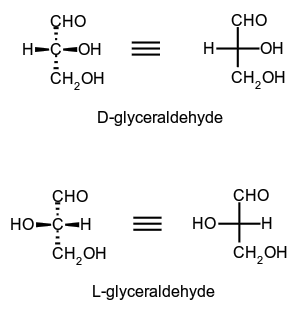
L-glyceraldehyde:https://molview.org/?cid=439723
D-glyceraldehyde:https://molview.org/?cid=79014
可以上molview網站實際觀看3D結構,拉拉看分子、旋轉擺弄
發現無論如何都無法將兩重疊,都差一點點、氣憤萬千
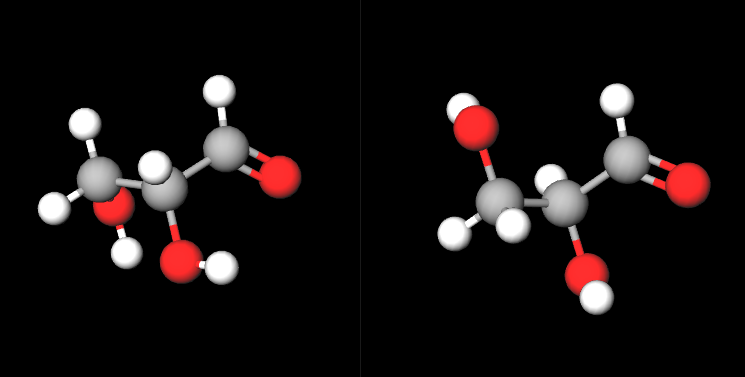
翻轉、旋轉、異構物數量
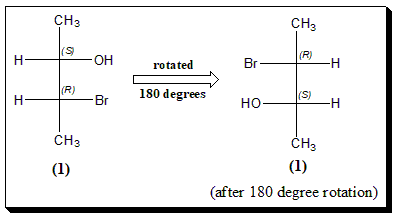
接下來的三種操作,對應到小畫家裡面的這三個操作:
水平翻轉、垂直翻轉、旋轉180°
這圖也十分奸詐,騙過了許多無辜清白的考生
看起來稍微將圖左右翻轉就可以得到,但這兩個是對映異構物
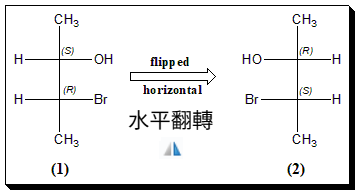
然而因為不能交換偶數次獲得(H與OH、H與Br,在不同的C*上
無法重疊就是無法
兩種異構物:
(2S,3R)-2-bromo-3-butanol:https://molview.org/?q=(2S,3R)-2-bromo-3-butanol
(2R,3S)-2-bromo-3-butanol:https://molview.org/?q=(2R,3S)-2-bromo-3-butano
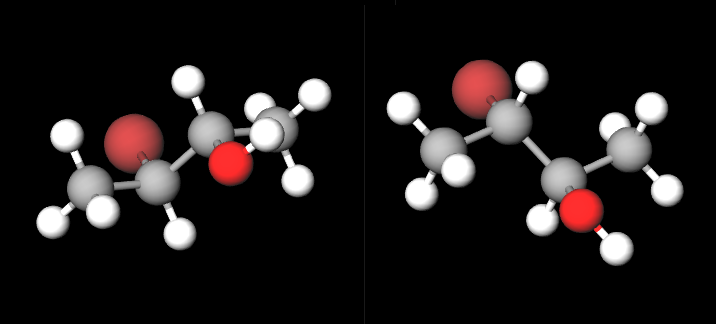
同一道題目
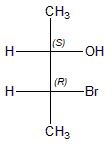
垂直翻轉(上下鏡像 Flip/Reflection),依然是得到對映異構物
兩種異構物:(2S,3R)、(2R,3S),這兩異構物依然與上面兩個相同
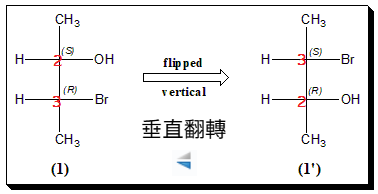
仍是同一道題目,這次則是將整張圖以180度旋轉(原圖扭頭由下往上看)
但是這次並沒有蹦出兩種異構物了!
旋轉180°看,並不影響整體結構,(2S,3R) 仍然是 (2S,3R),兩者是相同的!
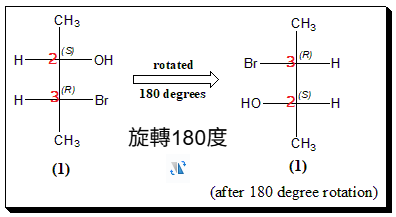
哦,既然旋轉180度能得原本構型,
你有發現之前的圖
「垂直翻轉」那張圖的右側分子 與 「水平翻轉」圖的右側分子
兩者可投過旋轉180度重合!這兩分子都是(2R,3S)
這時候來計算立體異構體數量,以此分子來說:
第2與第3碳上各有一個立體中心,所以總共有:2×2=4種立體異構體
分別為:(2S,3R), (2S,3S), (2R,3R), (2R,3S)
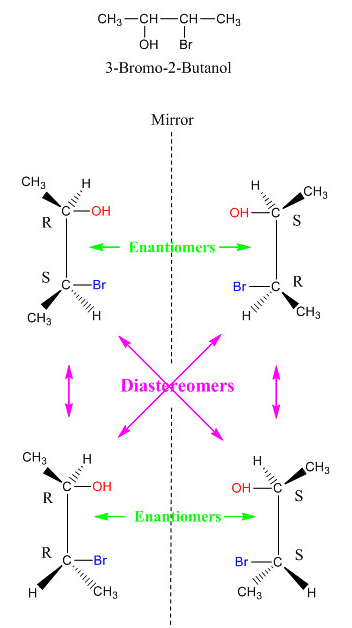
看不懂,前面到底在講些什麼?
如果難以理解的話(我最初卡關很久…後來悟通了)用以下例子來簡化比喻
「不能」直接把費雪圖形想成賽車骨架,將四個基團以四個車輪來想

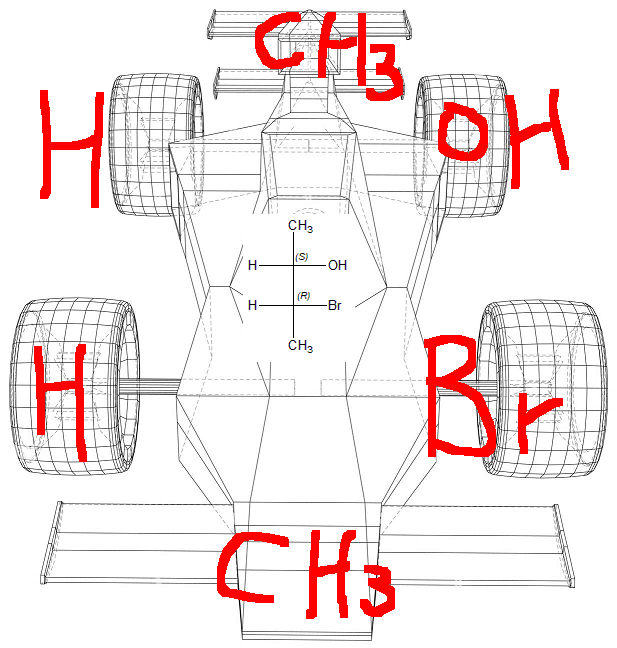
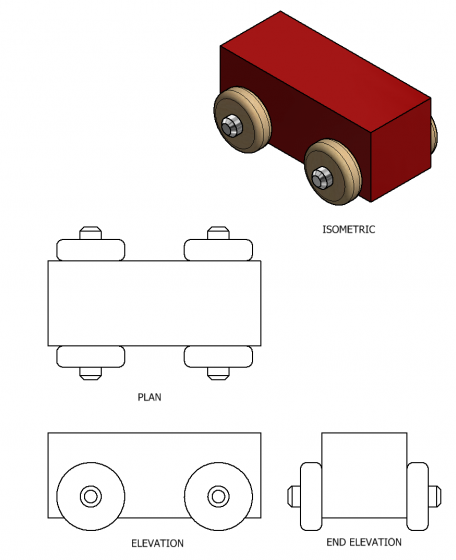
上面這種mapping思路是錯誤的!
而是要想成上面三腳架、下面也一個三腳架
而且腳位是上下錯開的(如左側),因為錯開電子間的斥力才是最小、最穩定
不是右側這種 三隻腳上下對稱的(電子斥力過大)
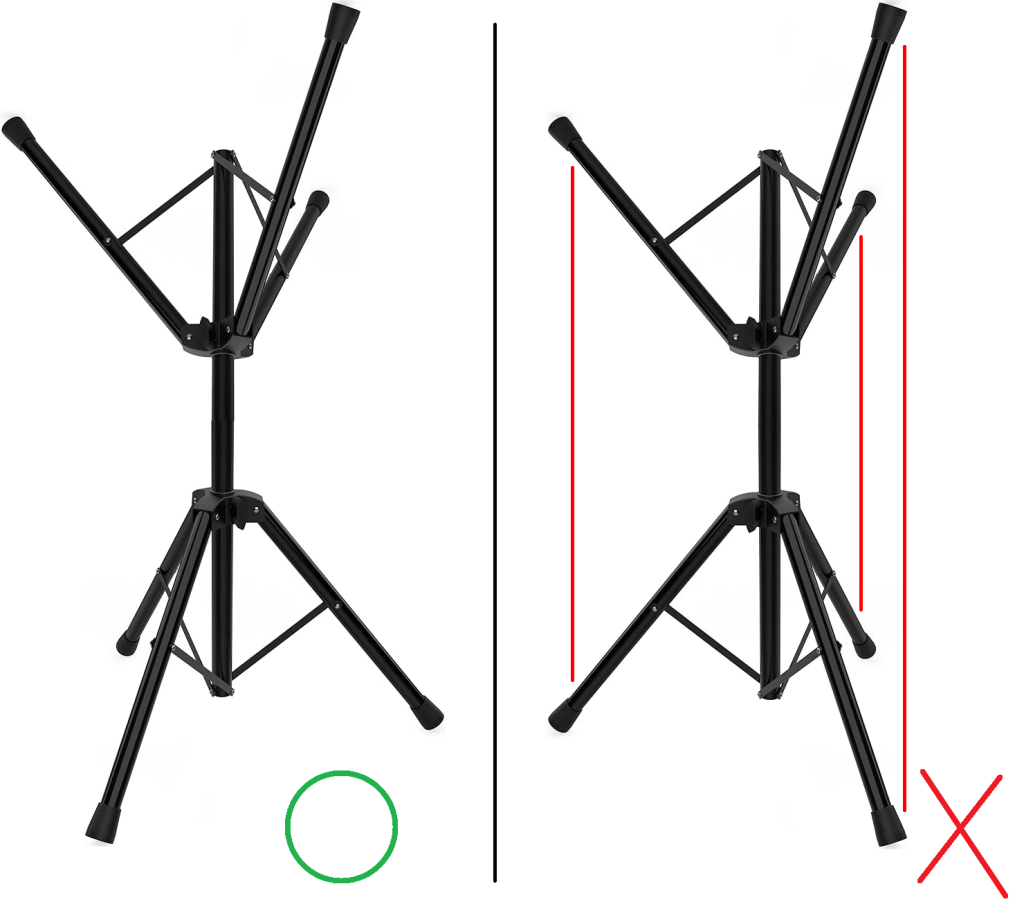
費雪投影是把這種立體空間,投影到看似平面的賽車車輪上。
雖以2D賽車骨架描述,但分子實際上仍是三維的!
真實結構仍有凸起來那一面,不是全然平的
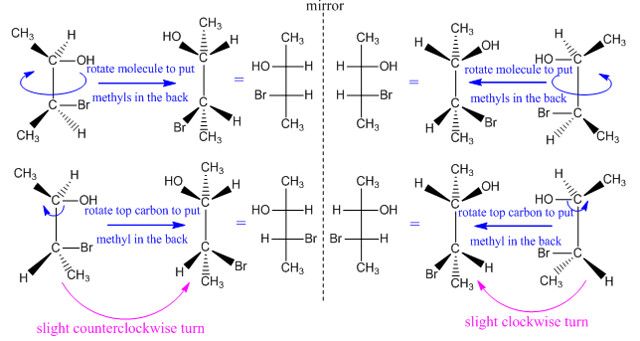
至於水平、垂直、旋轉三種操作,可以用手掌來比喻
手可以上下旋轉180度還是同一隻手
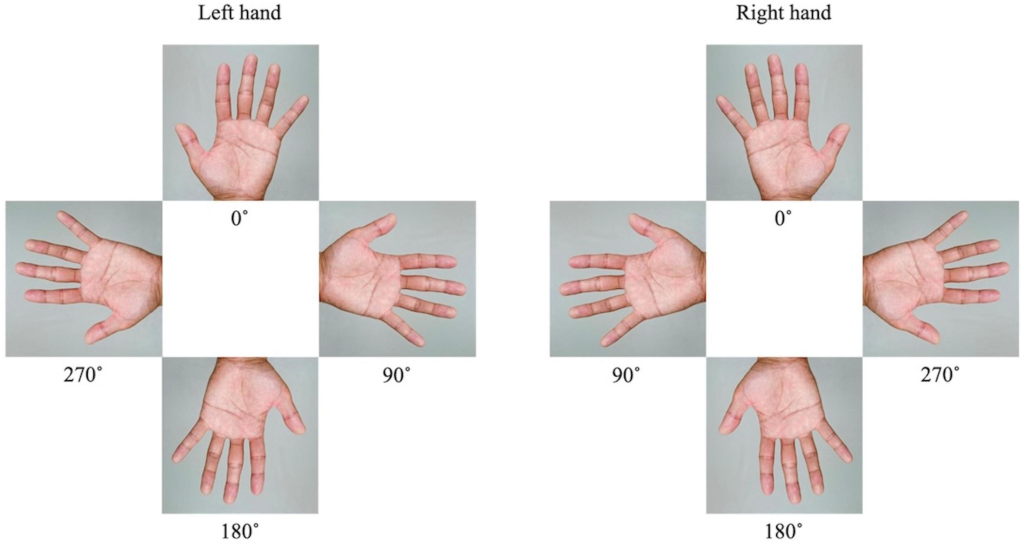
但是要水平、垂直翻轉,就得鏡像操作(透過鏡子)
而鏡像出來就是另一隻手
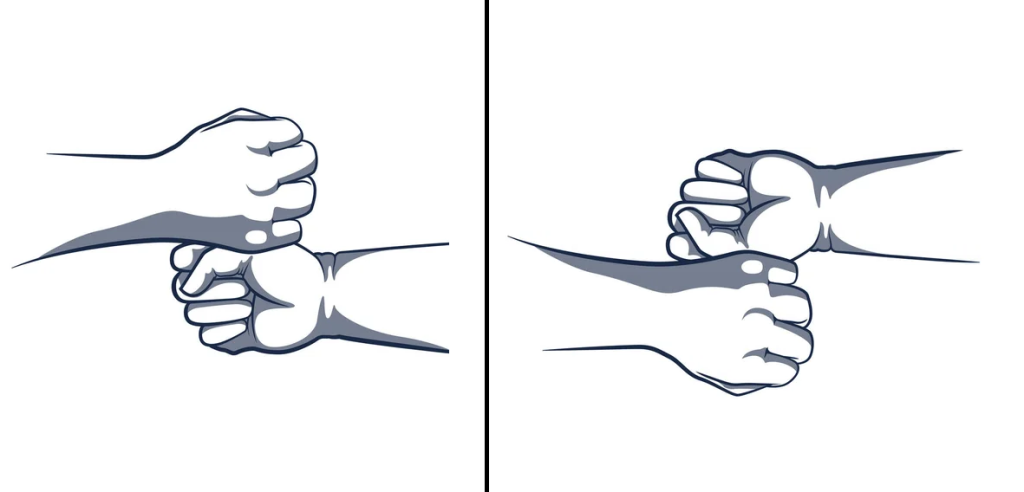
因為沒辦法用同一隻手,比出水平鏡像後的樣子,如下圖
手會爛掉

Meso 內消旋化合物
如果把前面分子的Br也換成OH(兩個都是OH),那麼就會出現meso(內消旋)化合物
記得前面說過,費雪投影垂直翻轉(上下鏡像 Flip/Reflection)後通常會是對映異構物
但改成這樣之後,上下鏡像得到的結果就一樣了,因為有翻沒翻費雪根本看不出來
原本 (2R,3S) 與 (2S,3R) 可疊合成同一個 meso 異構物,meso具有內部對映面
原先 2×2=4 種異構物,就會少一種可能性,於是 4 → 3
有點抽象?
現在想像成,今天這個分子就是兩坨東西,其中每一坨=「C上有 H、C、OH、CH₃四基團」
這坨東西組出來可以是左手、也可以是右手
將任意兩拳上下交疊在一起,那麼這坨分子有幾種組合?

預計會有4種排列組合:左+左、左+右、右+左、右+右
但是其中 「左+右」 可以顛倒過來看,變成 「右+左」⇒ 等同被meso掉了
所以自然消去一種,完全不同的僅剩下 「左左、右右、左右」 這三種組合
2,3-butanediol (2,3-丁二醇)
三種異構體分別為:(2R,3R)、(2S,3S)、(meso-2,3-butanediol)
實際構形
雖然費雪投影畫出來直挺挺的
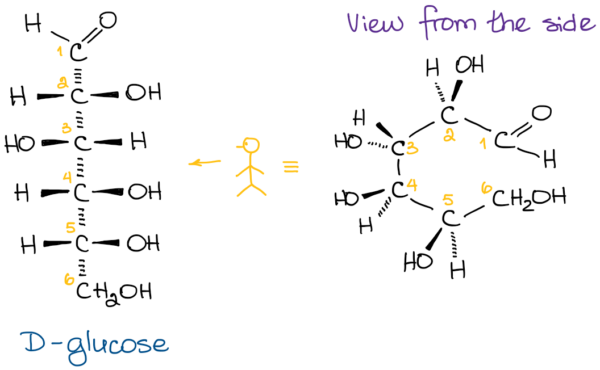
但實際上,碳鏈像是一條脊椎,構成一個彎曲的C字形
像一個人往前彎腰一樣
(因為費雪投影規定,近距離觀察每個碳時,C的上方下方的基團都要遠離觀察者。當多個C連在一起,自然而然就彎曲了)
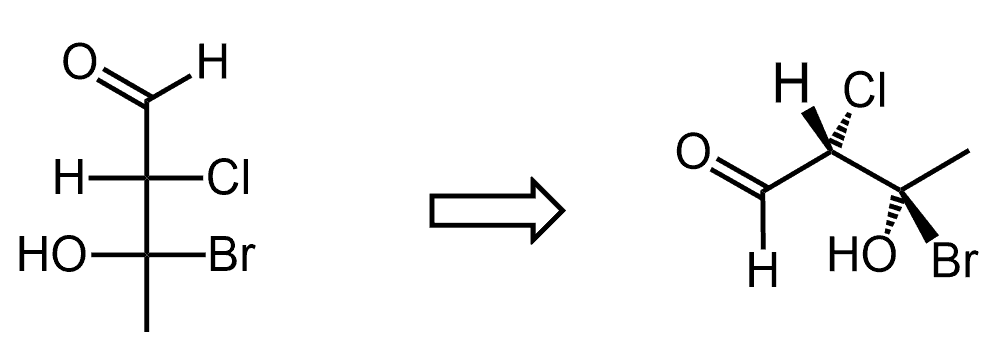
ZigZag (鋸齒狀)就是這種最常見的畫法
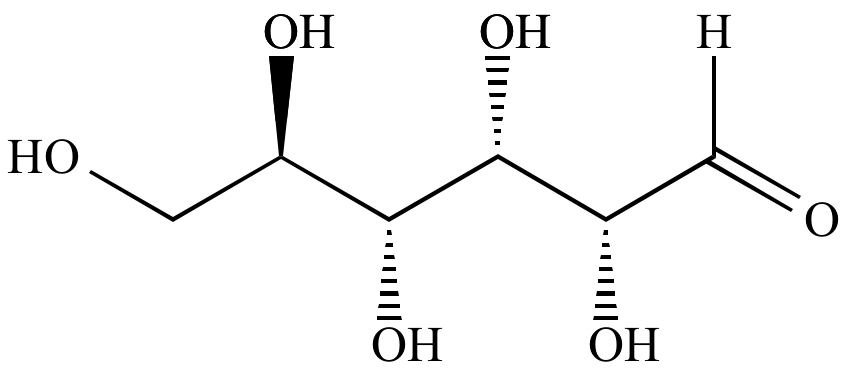
費雪投影若要轉成 ZigZag 構型,中間經過多個步驟:
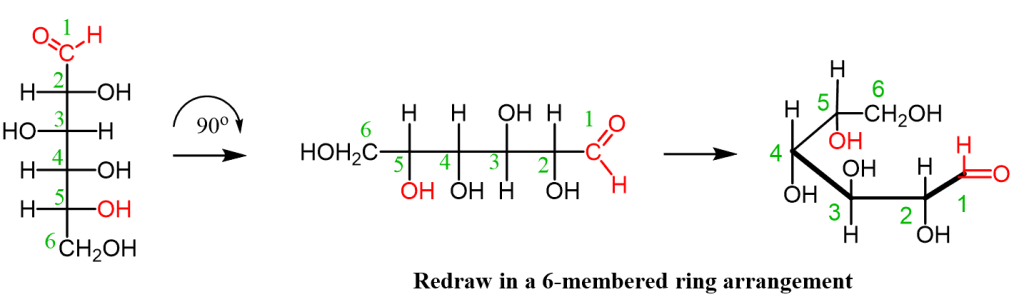
費雪投影 ⇒ 凹凸陰影(沒入/突出) ⇒ C字形 ⇒ Zig Zag構形
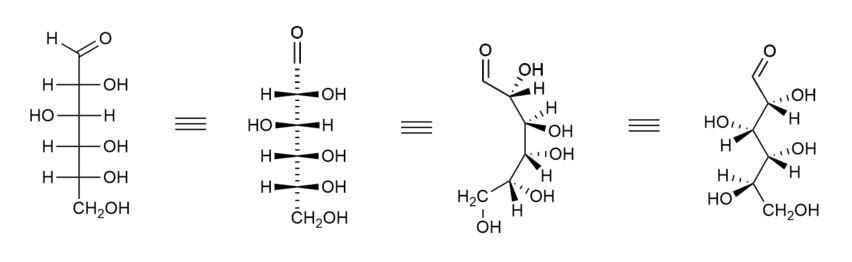
「C字形 ⇒ Zig Zag鋸齒構形」這一步驟要注意的是
在繪製時,左右基團一次要照抄、下一次要翻轉、再下一次照抄、再下下一次翻轉
為什麼要交替?
就像解開繩結、或者在旋轉鎖鏈鏈條一樣,後面鏈著的都會跟著連動

就像擰了很多圈的「米其林寶寶」為了恢復原狀、試圖扭回正
如果轉了半圈,寶寶會發現:左手在右、右手再左
再繼續轉半圈,寶寶會發現:左手、右手又回到原位置上了
=> 所以畫C字形 → Zigzag時,一次要翻轉左右基團、一次不用翻轉


發佈留言